Prefix Sum with HashMap can lower down Time Complexity from O(n²) to O(n)

Refering to LeetCode 560. A very clever way of using Prefix Sum with Hash-map is shown. In this post, I am going to break down this LeetCode question to reveal the idea of lowering down the time complexity by adopting Hash-map (or dictionary in Python).

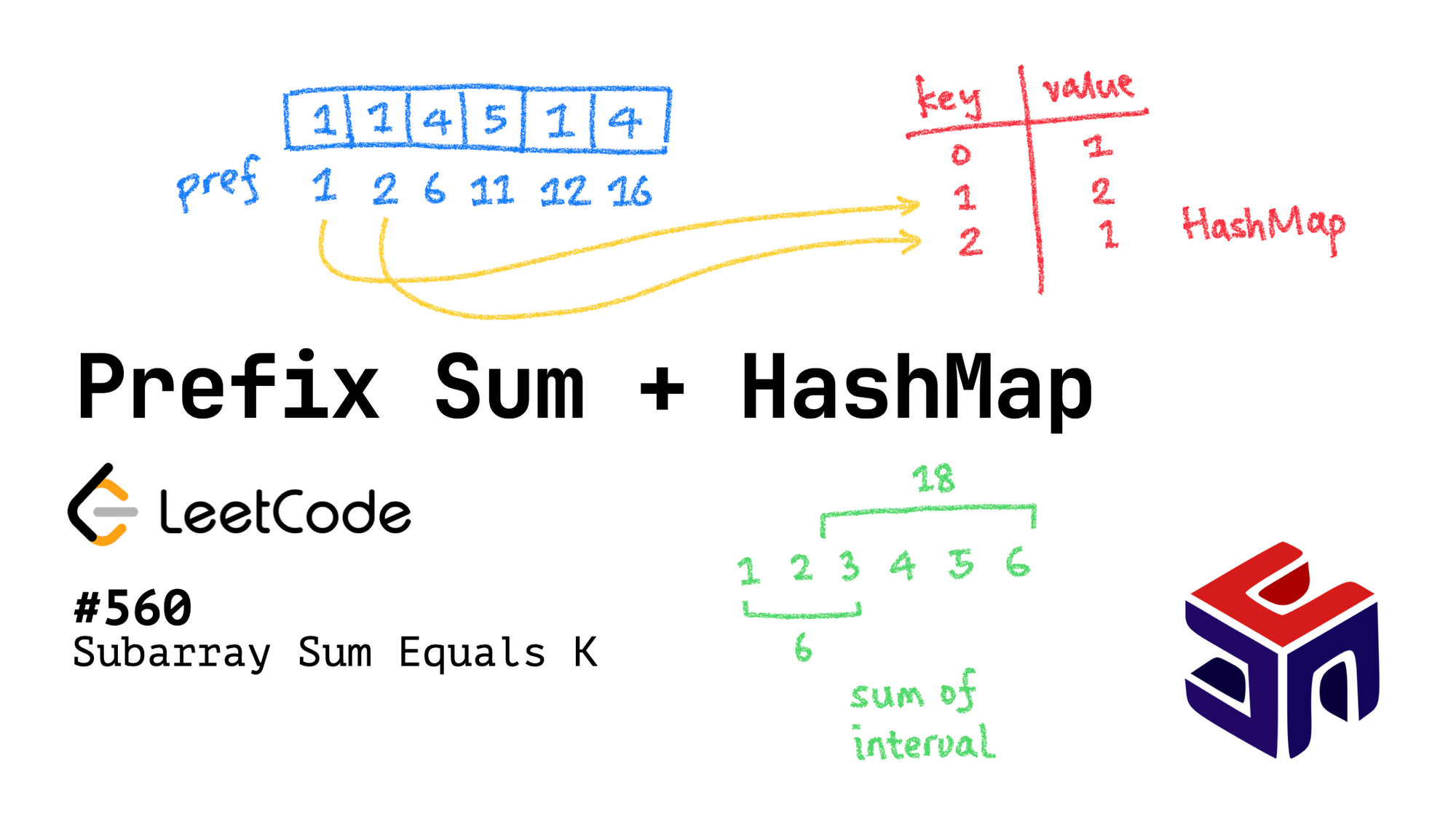
Reviewing question 560, an array nums and a target k is given to determine the number of sub-arrays res which having sum of interval equals k. Such that, giving array nums = [1, 1, 1, 1, 1, 1] and k = 4. The result res will be 3, target sub-array set contains nums[0:3], nums[1:4] and nums[2:5].

Adopting Prefix Sum

Since the time complexity of calculating sum of interval for a specific interval is $O(n)$:

for i in range(L, R):
  acc += nums[i]

If we want to calculate interval of sum more than one time, such as the problem 560, we should utilize Prefix Sum, which, $O(n)$ for constructing pref array and $O(1)$ for querying a specific interval, say [L, R]:

res = 0
pref = [0]

for i in range(len(nums)):
    pref.append(pref[-1] + nums[i])

# O(1) to query
interval_sum = pref[R] - pref[L]

Back to the Problem

In the problem, we need to check sum of intervals of each specific pair of L and R, since there are negative elements in nums.

The brute force code can be easily written using two for loop, which incurs a square time complexity $O(n^2)$.

for R in range(len(pref)):
    for L in range(R):
        if pref[R] - pref[L] == k:
            res += 1

From observation, we notice that:

When we considering each R, to find sum of interval starts with each L ranging from 0 to R, a linear time is needed to deduct the pref[R] by each pref[L].

Since scanning each pref[L] linearly is a little bit waste of time, so we can consider utilizing some spaces to trade time. We can adopt a dictionary (HashMap).

Consider that:

• In the inner for loop of L, we want to know how many L's can satisfy pref[R] - pref[L] == k, equivalent to pref[L] == pref[R] - k.
• We adopt a dictionary d to maintain number of L's having Prefix Sum as the key of d, hence d[i] means number of L satisfying pref[L] == i.
• Then we break the inner loop by res += d[pref[R] - k], that's wise, isn't it?
• Finally we update the dictionary d by the loop of R (refer to the following code).
• Note that we should initalize d by d = {0: 1}, think about why we should do so. (That is similar to we initialize pref using pref=[0]. Because there can be a sum of interval starting from the first element)

d = {0: 1}
res = 0

for i in range(len(nums)):
  pref.append(pref[-1] + nums[i])

for R in range(len(pref)):
  # number of intervals having sum k
  if pref[R] - k in d:
    res += d[pref[R] - k]
    
  # update d by right pointer R  
  if pref[R] in d:
    d[pref[R]] += 1
  else:
    d[pref[R]] = 1

We have cancelled out pref[L]. We can also discard pref[R]. The reason of it is R is in the outer loop, and it can totally combined with the previous loop for calculating pref. We also discard the pref array to make it calculate-on-use.

d = {0: 1}
res = 0
pref = 0

for num in nums:
  pref += num
  # number of intervals having sum k
  if pref - k in d:
    res += d[pref - k]
    
  # update d by right current num
  if pref in d:
    d[pref] += 1
  else:
    d[pref] = 1

Conclusion

We use a dictionary (HashMap) to replace the inner for loop for variable L, and we modify the code to eliminate the need for the 'pref' array. As a result, the time complexity is reduced from quadratic time to linear time. This technique is quite useful and can be applied to more LeetCode problems.