Binary Indexed Tree: A Data Structure that Can Enhance Query Performance in Arrays

Many years ago, I was a beginner in the Olympiad of Informatics. My friend @PremierBob taught me an incredible data structure that impressed me greatly: the Binary Indexed Tree, also known as the Fenwick Tree. It was a sunny afternoon at my high school.

Binary Indexed Tree

He noticed that I was quite bored, so he decided to come over and talk to me about algorithms. We were both preparing for the OI, so I appreciated.

He said, “If there is an array and I want to query the sum of a specific range, how would you do that?”

“A for loop,” the thought came to my mind. But he didn’t expect such a simple answer, apparently. “While you are definitely expecting a smarter way to do this, I’d rather know your approach,” I responded.

He started to introduce how integers are stored in a computer.

An Integer in Memory

The way of storing a positive integer in a computer is very straightforward. It is binary. Consider the number 42; its binary representation is 101010. Mathematically defined. Representing a negative integer is also very simple: just take the 2’s complement of the positive number. For example, -42.

42                   : 00101010
1's complement       : 11010101
2's complement (-42) : 11010110

“So the 1’s complement is just bit-wise NOT, and 2’s complement is the 1’s complement plus one?” I asked.

“Definitely!” he said.

“Wait a sec,” I was so confused. “What does this have to do with a range sum query of an array?”

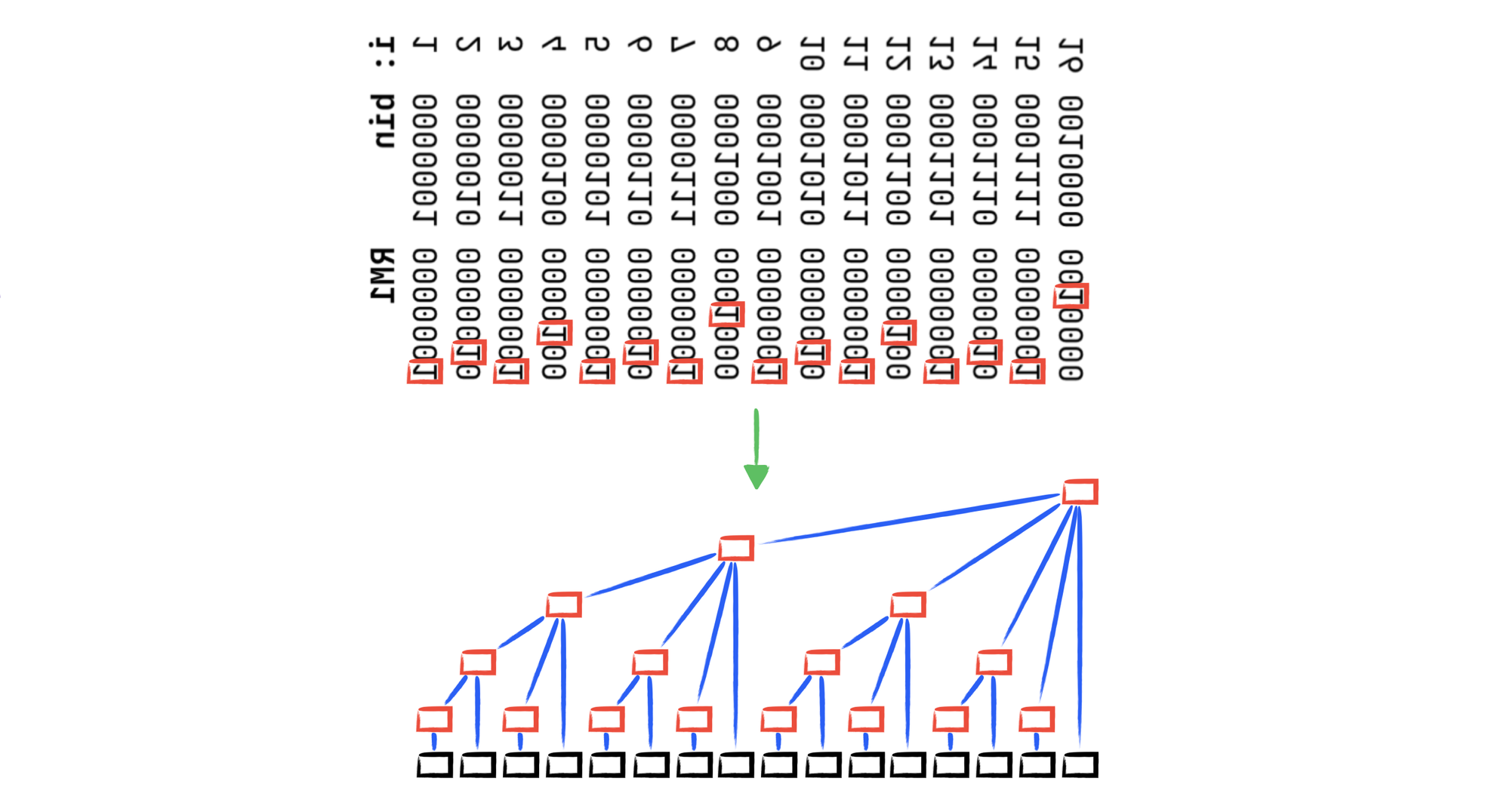
“Binary itself is the key to this approach. Let’s say the numbers from 1 to 16 are the index of an array, agreed?” he continued. “Just forget about 0 for now. If we just want the rightmost 1 (RM1) for these 16 numbers, what will that be?”

i: bin     RM1
1  0000001 0000001
2  0000010 0000010
3  0000011 0000001
4  0000100 0000100
5  0000101 0000001
6  0000110 0000010
7  0000111 0000001
8  0001000 0001000
9  0001001 0000001
10 0001010 0000010
11 0001011 0000001
12 0001100 0000100
13 0001101 0000001
14 0001110 0000010
15 0001111 0000001
16 0010000 0010000

“It is rarer to find the rightmost 1 on the higher digit than on the lower digit,” I responded. “And I know that the way of finding the rightmost 1 is bitwise AND for a number x with its negative value (-x).”

Find the Right Most 1 in a Binary

Simply calculate rm1 = x & -x and you will get that, see https://stackoverflow.com/questions/31393100/how-to-get-position-of-right-most-set-bit-in-c

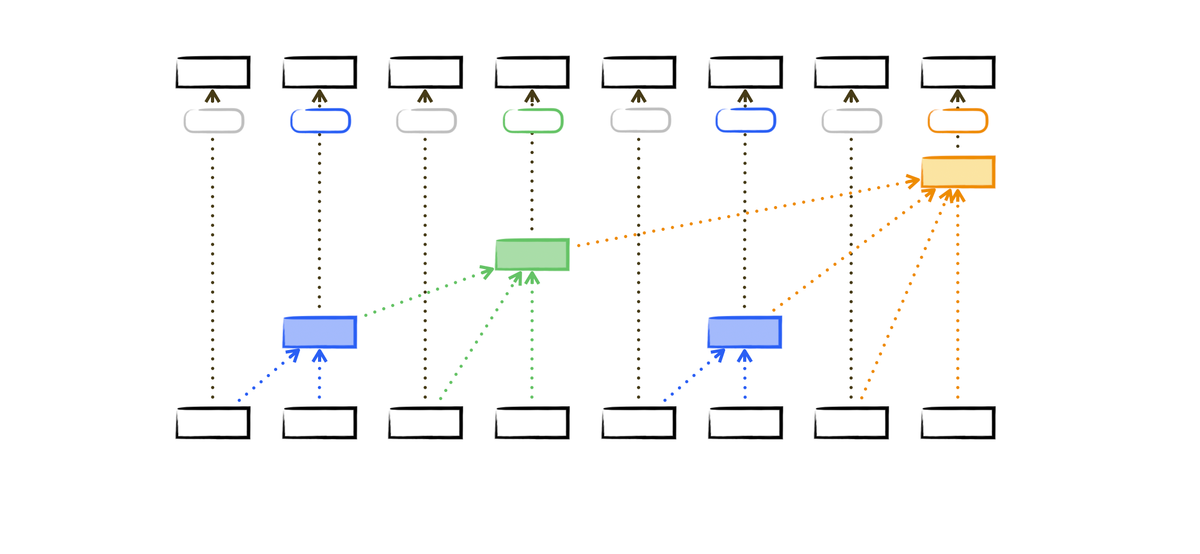
“That’s right, and it also follows some patterns. Let’s take a look at the following graph.”

“A red box contains the sum of all blue lines that extend from it.” he said while drawing, "with the nature of numbers, we can define this rule"

We named the function of finding the right most 1 as lowbit, the function is defined in code:

Array c maintains the sum of range such that starting from x - lowbit(x) + 1 and end with x, inclusively.

A code snippet to describe this rule is: c[x] = sum(a[x - lowbit(x) + 1, ..., a[x])

The following figure shows an example of maintaining an array a = [1, 2, 7, 6, 3, 5, 4, 1]. The array c = [1, 3, 7, 16, 3, 8, 4, 29] represents sum of each intervals in [[1, 1], [1, 2], [3, 3], [1, 4], [5, 5], [5, 6], [7, 7], [1, 8]], which is defined as [[x - lowbit(x) + 1, x], ...].

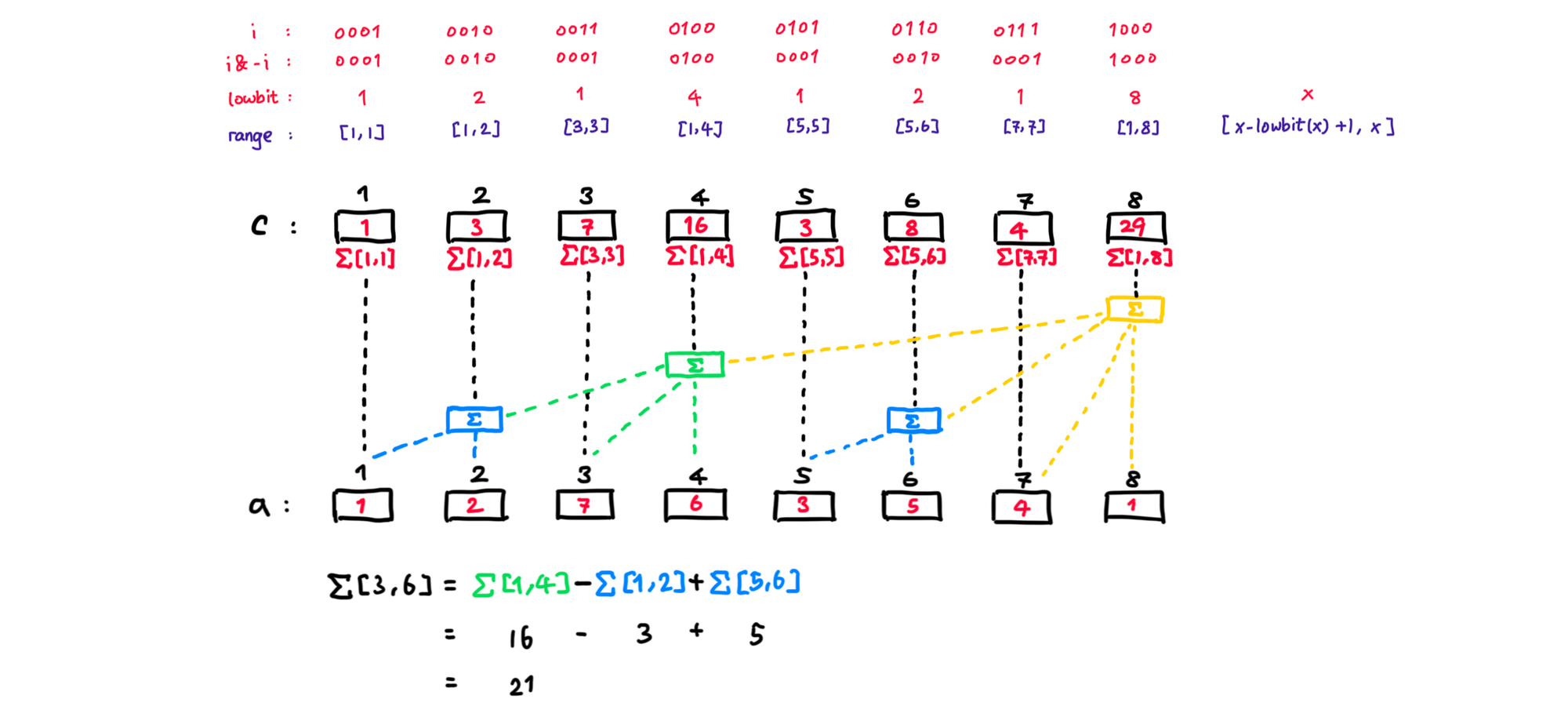
“That is awesome!” I said. “And you can query the sum of an array by adding these interval sums in c. For example, if I want to calculate the sum of the range [3, 6] inclusive, I just need to determine c[6] + c[4] - c[2], rather than calculate a[3] + a[4] + a[5] + a[6]. For a more extreme example, if I want to calculate the sum of the range [1, 8], I just use c[8].”

“This approach can lower the time complexity of determining the sum of a range from $O(n)$ to $O(\log n)$. But it’s worth mentioning that this approach only supports range arithmetic operations that follow the associative law, such as addition (sum), multiplication (cumulative product), and exclusive OR, aka XOR,” he added.

The Python code for getting the sum of an interval starting from 1 and the interval from l to r is:

To initialize the tree, we need $O(n)$ of time, we can use a prefix sum array sum, to help us with the initialization, then you can use the get_sum or get_sum_interval to query range sum.

Prefix Sum Array

A Prefix Sum Array, also known as a cumulative sum array or cumulative frequency array, is an array where each element represents the sum of all elements up to that index in the original array.

For example, given an array arr = [1, 3, 5, 7, 9], its prefix sum array would be [1, 4, 9, 16, 25].

The code is shown as follow:

"That's is clear, and what about updating the value at index i in a, like a[i]?" I asked.

"I will introduce that to you next time~".